II. Függvénytan

2.1. Függvényekről általában

Az orvosi munka során gyakran adódnak olyan problémák, amikor két tényező között kell kapcsolatot keresni (ok–okozat felderítése). A kérdést úgy is feltehetjük, milyen kapcsolat van az adott két halmaz elemei között? Mi az a matematikai konstrukció (formula), amellyel egymáshoz rendelhetjük a két halmaz elemeit? A kérdésre a választ a függvénytan adja meg.

Legyen X és Y a két vizsgálati halmaz. Célunk megtalálni azt a formulát, amely egymáshoz rendeli a két halmaz elemeit. A kapcsolatoknak csak azt a fajtáját vizsgáljuk, amelyben az egyik halmaz minden eleméhez hozzá tudjuk rendelni (úgyis mondjuk, hogy le tudjuk képezni) valamilyen módon a másik halmaz elemét. Az ilyen hozzárendelést nevezzük függvénynek (függvénykapcsolatnak):


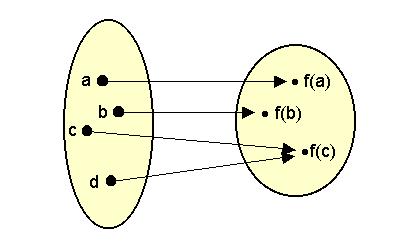
Függvényszerű kapcsolat ábrázolása.

Az első halmazt (X) a függvény értelmezési tartományának, a második halmazt (Y) pedig a függvény értékkészletének nevezzük. A biometriai vizsgálatok során csak olyan függvények fordulnak elő, ahol az értelmezési tartomány és az értékkészlet is a valós számoknak egy részhalmaza.

Az X halmaz elemeinek a leképezését a következőképpen szimbolizáljuk:

f: X Ž Y

ahol f jelenti a leképező függvényt. A szimbólumot úgy olvassuk, hogy f az X halmaz elemeihez hozzárendeli az Y halmaz elemeit. Más szóval az X halmazt leképezzük az Y halmazra és az Y halmaz elemeit (f(a), f(b), f(c)) képpontoknak nevezzük. A függvénykapcsolatot az

y = f(x)

megadási móddal jelöljük, ahol az x–t független változónak, y–t függő változónak nevezzük.

Természetesen előfordulhatnak olyan kapcsolatok is két halmaz elemei között, melyben az egyik halmaznak nem minden eleme rendelhető hozzá a másik halmaz valamely eleméhez, vagy pedig egy elemhez a másik halmazból több elem is megfeleltető:


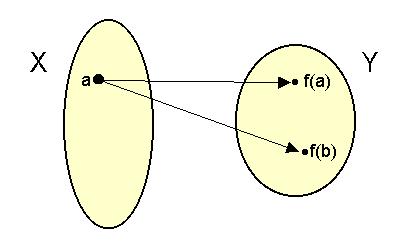
Nem függvényszerű kapcsolat ábrázolása

A biometriai vizsgálatokban ilyen jellegű kapcsolatokat nem vizsgálunk.

2.2. Leképezési eljárások

Két halmaz közötti hozzárendelést különböző módon lehet megtenni:

a) Injektív leképezés

Az X halmaz minden eleméhez hozzárendelünk egy elemet az Y halmazból. A hangsúly azon van, hogy két különböző X halmazbeli elem esetén a hozzájuk rendelt Y halmazbeli elemek is különbözők ( az X halmazt beleinjektáljuk az Y halmazba):


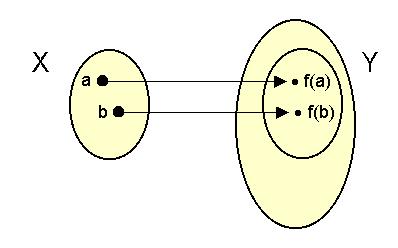
Injektív leképezés

b) Szürjektív leképezés

Az X halmazbeli elemek leképezésénél az értékkészlet maga az Y halmaz. Az X halmaz elemeit mintegy rátesszük (francia eredetű szó: sur (ejtsd szür)) az Y halmazra.


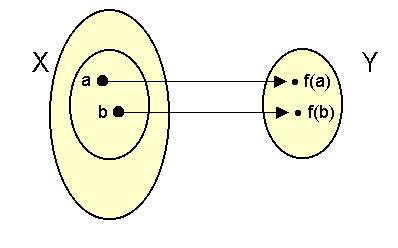
Szürjektív leképzés
c) Bijektiv leképezés

Ha az X halmaz leképezése egyszerre injektív és szürjektív is, akkor az X halmazt bijektív módon képeztük le. Ezt a leképezési eljárást kölcsönösen egyértelmű leképezési eljárásnak nevezzük.


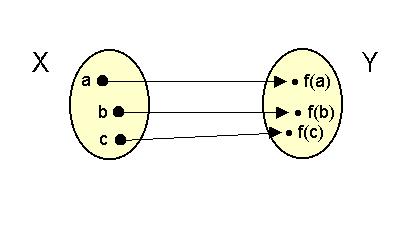
Bijektív leképezés

2.3. Függvény megadási módok

2.3.1. Táblázatos megadás

A megadás során többféle módon járhatunk el, de az egyik legegyszerűbb módja az összetartozó x és y értékek táblázatos formában való közlése és az értékek alapján a függvény megrajzolása a síkban. A függvény alakjának (vagy gráfjának) az ismerete hasznos információval szolgálhat a kapcsolat jellegéről. Az ábrázolásnál a jól ismert Descartes–féle koordináta rendszert használjuk a síkban. Az ábrázolás során a független változót az X–tengelyen, a függő változót a Y–tengelyen ábrázoljuk. Természetesen figyelemben kell venni, hogy minél több pontot ábrázolunk, annál pontosabb lesz a függvénykép.

2.3.2. Grafikonos megadás

A gyakorlatban a függvénykapcsolatnak ez egy ritkábban alkalmazott módja, inkább a műszeres mérésekre jellemző (EKG görbe)

2.3.3. Képlettel történő megadás

A leggyakrabban alkalmazott függvény megadási forma: a) Explicit forma: az egyenlet egyik oldalán az y, a másik oldalán az x–et tartalmazó kifejezés áll
y = f(x)
Ilyen az y = sin x kifejezés. b) Implicit forma: a megadott egyenletből az y nincs kifejezve. A megadási forma általános alakja:
F(x, y) = 0
Az F betűvel különböztetjük meg az implicit megadási módot az explicit formától.

Pl. a 6x2 + 4y + 6 = 0 függvény.

c) Paraméteres forma: ebben az esetben az x és y összetartó értékei egy harmadik mennyiség (egy paraméter) segítségével van megadva:
x = x(t) és y = y(t)
2.4. Inverz függvények

A gyakorlatban fontos az a fordított kapcsolat amikor a Y halmaz képpontjaiból kell meghatározni az X alaphalmaz elemeit:


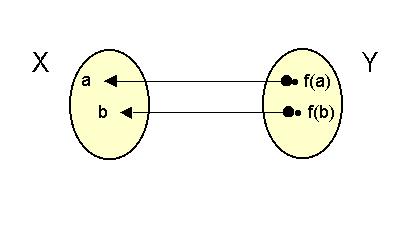
Inverz függvény hozzárendelés

Az ilyen kapcsolatot inverz függvény kapcsolatnak nevezzük Jelölése:

f –1: Y Ž X
vagy
x = f –1(y)

ahol a függvény független változója az eredeti függvény függő változója (y), értelmezési tartománya az eredeti függvény értékkészlete.

Egy függvény inverzét kétféle módon is meghatározhatjuk:

a) Az eredeti függvényből kifejezzük az x–et, majd ezt követően felcseréljük az x és y változókat.
Pl. határozzuk meg az 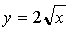 függvény inverzét. Először kifejezzük az egyenletből az x–et, ezért emeljük négyzetre mindkét oldalt:
y2 = 4x
innen az
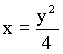A változókat felcserélve megkapjuk a keresett inverz függvényt.
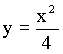b) Az egyenletben előbb felcseréljük a változókat és ezután az implicit alakból kifejezzük az y–t.
Pl. határozzuk meg az előbbi feladat inverzét ily módon is. Az első lépés a változók felcserélése:
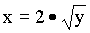Fejezzük ki az egyenletből y–t. Emeljük négyzetre mindkét oldalt:
x2 = 4y

innen

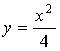Az x és y változók felcserélése egyben a koordináta–tengelyek felcserélését is jelenti. Ilyenkor az eredeti és az inverz függvény egymásnak tükörképei az origóból kiinduló y = x egyenesre (szimmetria tengelyre) nézve.

2.5. Függvények tulajdonságai

a) Monotonitás

Egy függvényt
  • monoton növekvőnek nevezünk egy tetszőleges (a,b) intervallumban, ha két tetszőleges

    • x1, x2 Î (a,b)–re igaz, hogy f(x1) <= f(x2) ha x1<x2;
  • monotoncsökkenőnek ha f(x1) >= f(x2).
  • Szigorúan monoton növekvő a függvény, ha f(x1) < f(x2) és
  • szigorúan monoton csökkenő, ha f(x1) > f(x2).
    •

    b) Korlátosság

    Egy y = f(x) függvényt alulról korlátosnak mondjuk, ha létezik egy olyan K szám, hogy a függvény értékére bármilyen x érték esetén igaz, hogy f(x) > K. Az y = f(x) függvény felülről korlátos, ha megadható egy olyan K szám úgy, hogy bármilyen x érték esetén az f(x) < K. Ha egy függvényre igaz, hogy alulról és felülről is korlátos, akkor a függvényt korlátosnak nevezzük. Ilyen pl. az y = sin x függvény.

    c) Periodicitás

    Az y = f(x) függvény periodikus, ha létezik egy olyan a>0 szám, hogy bármely x értékre és bármely egész k számra igaz, hogy f(x) = f(x+ka). Vagyis a függvényből kiemelhető olyan függvényérték, amely a szakaszonként ismétlődik. Az a szakaszt a függvény periódusának nevezzük. Ilyenek a szögfüggvények (a sin (x), cos (x), tg (x), ctg (x)).

    d) Páros tulajdonság

    Egy y = f(x) függvény páros függvény, ha a függvény képe szimmetrikus a y–tengelyre.
    Ez azt jelenti, hogy az f(x) = f(–x). Ilyen függvény az y = cos (x).

    e) Páratlan tulajdonság

    Egy y = f(x) függvény páratlan, ha a függvény görbéje szimmetrikus az origóra, ami azt jelent, hogy az f(x) = –f(–x). Ilyen függvény az y = sin (x) függvény.

    f) Konvexitás

    Egy függvényt konvexnek nevezzük egy adott intervallumon, ha a függvény bármely pontjához rajzolt érintőt a függvény “alsó korlátjának” tekintjük.
    Egy függvényt egy adott intervallumon konkávnak nevezzük, ha a függvény bármely pontjához húzott érintőt a függvény “felső korlátjának” tekintjük. Az adott intervallumon a függvény alatta van az érintőnek.

    2.6. Összetett függvények

    Az olyan függvényt nevezzük összetett (közvetett) függvénynek, ahol a független változó egy másik függvénynek a függvényértéke. Pl. az y = cos x2 ilyen függvény. A függvényértékét úgy határozzuk meg, hogy adott x esetén először elvégezzük a hatványozást, majd ennek az értéknek vesszük a koszinuszát.

    2.7. Függvényvizsgálatok

    A biometriai vizsgálatok során előfordulnak olyan esetek, amikor egy vizsgálat során rendelkezésünkre áll ugyan egy függvénykapcsolat formája, de többet szeretnénk tudni magáról a függvényről. Ilyen esetekben ún. függvényanalízist kell végezni, amely magasabb fokú matematikai apparátust használatát (differenciálszámítás) igényli. Egyszerűbb analitikus vizsgálatok közé tartozik:
    •  a függvény értelmezési tartományának meghatározása,
    •  a x és y tengelyek metszeteinek kiszámítása,
    •  folytonosság, szakadási helyek,
    •  határérték meghatározása.
         Nehezebb analitikus vizsgálatok, amelyek révén megállapíthatjuk a görbe jellegzetes pontjait:
    • a függvény maximuma és minimuma,
    • inflexiós pontok (a függvény görbéje konvexből konkávba vagy konkávból konvexbe fordul),
    • határérték számítás,
    • a függvény értékkészletének meghatározása.

    2.8. Elemi függvények

    2.8.1. Racionális egész függvények

    Explicit formában az általános alak:
    y = a0 + a1x + a2x2 + ... + an–1xn–1 + anxn
    ahol az a0, a1, a2, ..., an tetszőleges valós számok. A kifejezésben csak összeadás, kivonás és egész kitevőjű hatványozás szerepel. Az ilyen kifejezéseket polinomoknak is hívjuk.

    Speciális esete az elsőfokú vagy lineáris függvény. Kitüntetett szerepe van a biometriai vizsgálatokban a függvénytípusnak:

    y = a + bx
    ahol a és b valós számok. A függvény alakja egy egyenes és a b értéke jelenti az egyenes meredekségét (az egységnyi x érték növekedésre eső y érték változását jelenti), az a érték pedig a tengelymetszet magasságát. Ha a kifejezésben az a = 0 (nulladfokú függvény), akkor egy konstans függvényt kapunk, mely párhuzamos az X tengellyel és az Y–tengelyt az a értéknél metszi. Ha a = 0, akkor az egyenes átmegy az origón és a függvény az x és y változók közötti egyenes arányosságot fejezi ki:


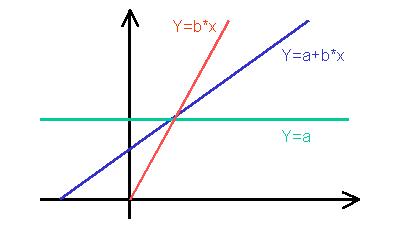
    Az y = a + bx lineáris függvény alakjai

    A polinomok fontos képviselői a másodfokú polinomok, melyek általános alakja:

    y = ax2 + bx + c     ahol a š 0
    Az ilyen típusú egyenletek parabola alakúak, s az a értékétől függően változtatjuk helyzetüket:

    2.8.2. Racionális törtfüggvények

    A racionális törtfüggvények két racionális egész függvény hányadosaként adható meg azzal az általános feltétellel, hogy az adott forma tovább már nem egyszerűsíthető:
    y =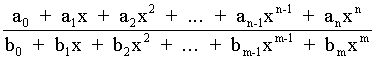 
    A legegyszerűbb racionális függvény a hiperbola: .

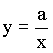    2.8.3. Irracionális függvények

    Azokat a függvényeket, amelyek explicit alakjában a gyökjel alatt az x értéke is szerepel, irracionális függvényeknek nevezzük. Ilyen függvény pl. 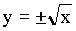 függvény is, ami az y = x2 függvény inverz függvénye.

    2.8.4. Transzcendens függvények

    Legegyszerűbb formája az exponenciális függvény, melynek általános alakja:

    y = ax

    A függvény alakja:


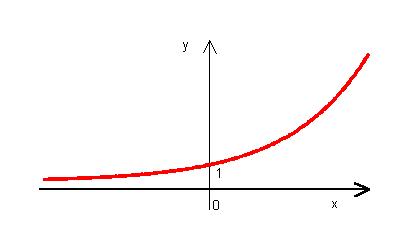
    Az y = ax függvény képe

    Különösen fontos szerepe van az élő szervezetek vizsgálatában az y = ex függvénynek. Az e az Euler–féle szám, amelynek értéke ť 2.718. A természetes alapú logaritmusnak is ez az érték az alapszáma.

    Az exponenciális függvény inverz függvénye a logaritmus függvény:

    y = logax

    ahol a > 1.


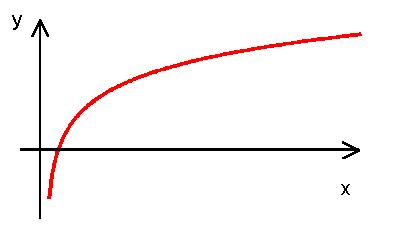
    Az y = loga x függvény grafikonja a > 0 esetén

    A trigonometrikus függvények inverz függvényei az árkusz függvények, amelyek többértékű függvények. Az y = sin x függvény inverz függvénye az y = arc sin x, az y = cos x inverz függvénye az y = arc cos x, az y = tg x függvény inverz függvénye az y = arc tg x és az y = ctg x függvény inverz függvénye az y = arc ctg x függvény. Ha csak egy periódusát, a főértékét vizsgáljuk ezeknek a függvényeknek, akkor azt a megkülönböztetés végett nagybetűvel jelöljük pl. y = Arc sin x függvény.
     

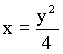
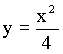
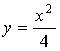
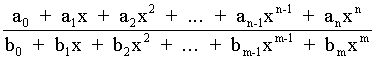
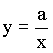    Feladatok