Feladatok
1 , 2 , 3 , 4
, 5 , 6 , vissza a függvényekhez
1. Vegyük a sin: X --> Y függvényt,
ahol Df jelöli a függvény értelmezési tartományát.
| |
X
|
Df
|
Y
|
| a) |
(0 , p /2)
|
(0, p /2)
|
(0, 1)
|
| b) |
[-p /2, p
/2]
|
[0, p /2]
|
[0, 1]
|
| c) |
[0, p /2]
|
[0, p /2]
|
[0, 1]
|
| d) |
[-4, 2]
|
[-4, 2]
|
[-1, 1]
|
2. feladat
Legyen két függvény a g: A -->
B és a f: B --> C.
Létezzen az f-1, g-1, f ° g valamint a g-1
° f-1 függvény.
Igaz-e a következő állítás:
(f ° g)-1 = g-1 ° f-1
3. Az alábbi ábrán az f, g, h bijektív függvények
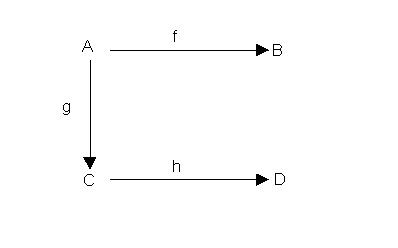Adjuk meg a y : D --> B
bijektív függvényt.
4. feladat
Egy A populáció minden egyedéhez rendeljük hozzá az összes tőle különböző,
vele rokonságban álló egyedet. Függvényt ad-e az olyan leképezés, ha az
értékkészlet
a) az A halmaz
b) az A összes részhalmazainak a halmaza
c) invertálható-e a függvény
5. Határozzuk meg az y = 2Ö
x függvény inverzét.
6. feladat
Határozzuk meg az
f: x --> Ö 2x (x Î
[0, 8 ))
függvény inverzét.