Variancia analízis
Történet , Elvi
alapok , terminológia , Terv
, Transzformációk , H0
, Modellek: I vagy II ,
ANOVA tábla ,
Többszörös összehasonlítás módszerei:
tervezett és
post hoc összehasonlítások ,
Képletek
Bevezetés
Példa: Szövettenyészetben tartott melanotróp mirigysejteken vizsgálták különböző
életkorok hatását a sejtplazma szabad kalcium szintjére. A sejtplazma kalcium
szintjét fluoreszcens festék segítségével optikai módszerrel folyamatosan
regisztrálták és az átlagos koncentrációt sejtenként feljegyezték.
Az így kapott érték minden sejtre egy értéket adott. Összesen 409 sejtet
vizsgáltak, és életkoronként 48 - 302 sejten végeztek megfigyeléseket.
Az eredményeket az alábbi táblázatban foglaltuk össze.
1. táblázat. Az életkor hatása a melanotróp sejtek citoplazma
kalcium szintjére
(Némethy et al. 1999)
|
Életkor
|
Kalcium szint (nMol/L)*
|
esetszám
|
|
2 napos
|
156,5+-12,1
|
59
|
|
10 napos
|
187,2+-3,9
|
302
|
|
40 napos
|
222,8+-13,4
|
48
|
* átlag +- az átlag hibája
Ez a legegyszerűbb többcsoportos vizsgálat, melyben 3 egymástól függetlenül
vett minta értékeit vizsgáljuk és hasonlítjuk össze.
Ha a vizsgálati eredmények olyan minták, melyek eloszlásáról ismereteink
alapján feltételezhetjük, hogy megfelelnek a paraméteres statisztikai elemző
módszerek kiinduló feltételezéseinek, akkor a legegyszerűbb esetben 2 mintánk
van. Két minta esetében azok átlagának eltérése (valamelyik) t próbával
elemezhető.
Ebben az összetettebb esetben 3 mintánk van, melyek egyidejű vizsgálata
indokolt.
Ilyenkor nem ismételjük az egyszerű esetben használt eljárást ( t
próba) minden lehetséges, vagy a kutatás számára érdekes összehasonlítás
elvégzésére, helyette együtt vizsgájuk a minták tulajdonságait:
-
a több minta azonos populációból ered-e?
-
más szóval: a több csoport között van-e különbség? (átlagok, esetleg variancia
különbözősége)
Az általánosítás egyik módja az ANOVA használata.
(Terminológia: Szórás elemzés, Variancia analízis, analysis of
variance=ANOVA)
Az ANOVA-k csoportosíthatók egyszempontú, több szempontú,
hierarchikus, random blokkos, több dimenziós ANOVA-kra, valamint regresszió, és
kovariancia analízisekre.
Miért jobb egy ilyen kísérleti terv, mint a két, vagy több független kísérlet
elvégzése, a több t próba alkalmazásával folyó kísérletezés?
-
Lehetővé teszi a kontroll és az N (=2) kezelés egymáshoz hasonlítását is,
kísérletenkénti
korrekt elsőfajú hibával ( a
).
-
Gazdaságosabb az erőforrások felhasználása, nem kell kísérletenként külön
kontrollt használnunk.
-
Jobb a csoportokon belüli szórás becslés, mert azt több megfigyelésre
alapozhatjuk, más szóval pontosabb becslést kapunk a populációról.
-
további előnye: a hatások kombinációban történő együttes tesztelésének
lehetősége. Jó hatásfokú módszerek állnak rendelkezésünkre a kísérletenkénti
szignifikancia szint melletti hipotézisvizsgálatra.
Története
Az ANOVA alkotója R.A. Fisher (egy angliai mezőgazdasági kísérleti állomáson).
Zseniális felismerése: Több csoporton együtt végzett kísérletben a null
hipotézis, H0 úgy is vizsgálható, hogy
kiszámítjuk (egymástól függetlenül) két módszerrel a populáció varianciájának
becslését. Egyik módszerrel a csoportokon belüli szóródásból, a másik
módszerrel a csoportok közötti szóródásból.
H0érvényessége esetén a kettő ugyanannak
a mennyiségnek két becslése. Ha ez nem valószínű, akkor arra következtetünk,
hogy a H0 elvetendő: azaz a csoportok
között van különbség. A különbség lehet az átlagokban, vagy a szórásban.
Elnevezés: nem szerencsés, "misnomer". Valójában additív faktorokat
vizsgálunk, a varianciák elemzésének eszközét felhasználva, tehát az analízisnek
nem célja, hanem eszköze a varianciák elemzése.
Lap teteje
Az eljárás lényege, elnevezések, konvenciók.
Az első lépésben arra vagyunk
kíváncsiak: van-e különbség a csoportok között, vagy pedig azok mind egy
populációból származó minták? Más szóval: elvetjük-e a H0
-t, vagy a H0 -t érvényesnek tekintjük, mert nem vetjük el
A minta elemek szórásának vizsgálata során először a négyzetes eltéréseket,
majd az összegzett négyzetes eltéréseket vizsgáljuk. Az "átlagos" négyzetes
eltérés a variancia, ennek négyzetgyöke a szórás (standard deviáció).
A mintaelemekből számított teljes négyzetes összeg olyan N-1
összeadandóból áll, amelyek egyes tagjai a szóródást létrehozó különféle
tényezőkről, "okokról" tájékoztatnak. A négyzetes összeg particionálható,
felbontható (additív) komponensekre. (Az átlagolt négyzetes összegek
(variancia=szórásnégyzet) nem additívak, hanem súlyozottan átlagoltaknak
minősíthetők.)
Osztályozó (csoportosító) változónak nevezzük azt a változót (független
változó), mely tartalmazza a kísérletező által meghatározott beavatkozások
jellemzőit.
Függő változó(k) tartalmazza(k) a mért, vagy megfigyelt adatokat; minta
értékeit.
Elkerüljük az adatok külön oszlopokban történő megadását, ilyent csak a blokk
elrendezés esetén ("repeated measures") használunk. Ennek okai:
-
bár 1 szempontnál (egyszeres osztályozás) szemléletes, de nem segít, sőt
hátráltat a kettő vagy több szempontnál.
-
ellentétben áll a legtöbb statisztikai program gyakorlatával
-
Nehezen általánosítható, 3 vagy 4 szempont esetében igen nehézkes lenne.
Lap teteje
Terminológia
-
Egy kísérleti egység - egy megfigyelés, egy sor.
-
Egy függő változó - egy oszlop
-
Csoportosító változó - független változó (angol szakszövegben: grouping variable;
independent variable)
-
Egy csoportosító változón belül annak különböző szintjeiről beszélünk (angolul:
level). A különböző kezeléseket, ugyanazon faktor különböző szintjeinek mondjuk.
A szinteket kódokkal jelöl(het)jük.
Később tárgyaljuk a kettős csoportosítás, két csoportosító változó, többes
csoportosítás, több csoportosító változó eseteit.
Az egy szempontú ANOVA-nál általában igaz, hogy az egyes minták, csoportok
elemszáma lehet változó, a hiányzó adatok nem zavarnak az elemzésben, az
egyenlőtlen elemszámokra is van könnyen számolható képlet. Azonban az ANOVA után
alkalmazott többszörös páros összehasonlítások közül azok, amelyeknél az egyes
csoportok szórása és elemszáma nem kerül felhasználásra, kiértékelésre, azok
hiányos adatok, nem szimmetrikus elrendezés esetében hibás következtetésekre
vezethetnek.
Lap teteje
A kísérleti terv
-
Meghatározzuk az alkalmazandó kontroll eljárást, a kezelések adagját,
körülményeit.
-
Kiválasztjuk az egyes csoportok elemszámait, a véletlenszerű kezelés
hozzárendelés szabályait.
-
Megtervezzük a kísérlet utáni kiértékelés módszereit, ellenőrizzük, hogy a
kísérleti elrendezés és a tervezett kiértékelés összhangban van-e?
-
Kiválasztjuk az alkalmazandó "páros", vagy többszörös összehasonlításokat.
-
Meghatározzuk az alkalmazandó szignifikancia szintet.
-
Elvégezzük a kísérletet, az adatgyűjtést.
-
Ellenőrizzük az adatok minőségét. Vizsgáljuk az adatokat (exploratory data
analysis)
-
Ellenőrizzük a kiinduló feltételezések teljesülését.
-
Elvégezzük az analízist.
Lap teteje
Feltételek
-
Normális eloszlás
-
véletlen mintavétel
-
a hiba varianciák függetlensége
-
a varianciák homogenitása, egyformasága (homoscedaszcitás)
Ezek a feltételek a H0 érvényessége esetében (triviálisan)
teljesülnek.
A feltételek teljesülése vizsgálandó. Eszköze az adatelemző grafikus
ábrázolás (EDA), az előzetes statisztikai tesztek.
A feltételek nem teljesülése esetén mit tegyünk? Az ANOVA robusztus eljárás,
azaz a feltételek kisebb-nagyobb mértékű nem teljesülése nem rontja el a
következtetések érvényésségét, nem növeli meg jelentősen a hibás döntések
számát. Ezzel azonban nem szabad visszaélni!
-
Véletlen mintavétel Tőlünk függ.
-
Normális eloszlás. Gyakran a mintából nem dönthető el. Viszonylag nagy
elemszám kell a megbízható vizsgálatához, hosszabb tapasztalat, irodalmi
ismeretek alapján lehet véleményezni. Nagy elemszámoknál segít a centrális
határelosztás tétele.Vizsgálatára az egyes csoportokon belüli residuális-okat
képezünk, és teszteljük eloszlásuk normalitását.
-
A minták függetlensége. Összefüggő adat csoportok esetében a függőség
jellege szerint kell a statisztikai eljárásokat megválasztani. Az egyszempontos
ANOVA esetében a kísérlet, a mintavétel és a mérés tervezése során kell
biztosítani a mintákat alkotó adatok függetlenségét.
-
A variancia egyformasága (homogenitása). Ellentéte a heteroscedascitás, a
varianciák inhomogenitása. A kísérleti csoportokon belüli variancia a
viszonyítási alap, ehhez mérjük hozzá a csoportok közötti átlagos
négyzetösszegeket, vajon ez utóbbiak lehetnek e a populáció varianciájának
becslései.Az ANOVA erre (is) robusztus.
Egy kivétel: Korrelált átlagok és szórások. Sok csoportból kevésre egyszerre
igaz, hogy például nagy átlagú és nagy szórású. A veszély oka: a nagy szórású
átlag bizonytalan becslést ad. Ez lehet jelentősen gyengébb, mint az átlagos
variancia alapján készített becslés, így erre vigyázni kell.
Lap teteje
Transzformációk
Ha az adatok vizsgálata során kiderül, hogy a varianciák homogenitásának
feltétele nem teljesül, akkor az első teendőnk annak vizsgálata, hogy
transzformálással elérhető-e a varianciák homogenitása?
Ha a minták szórásai úgy viszonylanak egymáshoz, mint az:
| átlagaik négyzetgyöke, akkor |
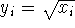 |
a megfelelő transzformáció |
| átlagaik, akkor |
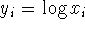 |
a megfelelő transzformáció |
| átlagaik négyzete, akkor |
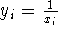 |
a megfelelő transzformáció |
A transzformációk gyakran a mintának több, az ANOVA kiinduló feltételezéseit
megsértő tulajdonságát egyszerre közelítik a feltételezettekhez.
A transzformáció és az additivitás viszonya: esetenként átgondolandó. A
visszatranszformálás ezekben az esetekben lehetséges. A transzformált adatok
használatánál a kezelések additivitása az ANOVA modelljében mást jelent, mint az
eredeti adatok esetében. Ez különös súllyal veendő figyelembe akkor, ha az ANOVA
nullhipotézisét elvetjük, és az egyes minták különbségeit kezdjük vizsgálni.
Lap teteje
Az egyszempontú ANOVA nullhipotézise
n csoport esetén, ha m-el az átlagokat jelöljük, akkor
H0 = m1, m2, m3, ... ,m n
átlagok mind egy populáció várható értékének becslései.
Az alternatív hipotézis. HA = m1, m2 , m3,
... ,mn átlagok nem mind egy populáció várható
értékének becslései. Másképen fogalmazva, az átlagok közül legalább 1 nem a
többi minta populációjából származik. Azaz a minták legalább két (de lehet, hogy
több) populációból származnak-
A modell
Minden egyes adat modellje (összetevői): Adat = (nagy átlag) + (kezelési
átlag) + szórás (reziduális, véletlen tényező)
Eljárás, alapelv
Az adatok összes szóródását mérő variancia (szórásnégyzet) különböző elemeket
tartalmaz. Más szóval az összes szóródás specifikus jelentést hordozó
összetevőkre bontható. Ha a null hipotézis teljesül, akkor minden független
komponens ugyanazon populáció szórásának a független becslése.
Itt a variancia kiszámításánál használt
négyzetes összeg felbonthatóságának tételét alkalmazzuk.
Megjegyzés: a négyzetes összeg a távolság mérték jellegzetes és
intuitíven megszokott tulajdonságaival rendelkezik.
Az egyik lehetséges felbontás: A csoportokon belüli szórás összevonható, és a
közös szórásbecslés ugyanannak a populációnak a szórását becsüli, mint az
átlagokból származtatott szórásbecslés, ami az adatmodellben a (kezelési átlag)-ok
szóródása. A nullhipotézis teljesülése esetén a a kezelési átlagok valódi
értékei mind nullák! Szóródásukban csak a minta véletlen szóródásból eredő
változékonysága jelentkezik.
A két szórásbecslés hányadosa, mint statisztika az F eloszlást
követi (a számlálóban és a nevezőben lévő szórásbecslések szabadságfokaival
jellemzett F eloszlást).
Ha az F statisztika értéke nagyobb vagy egyenlő az eloszlásból
számított küszöbértéknél, akkor a null hipotézist elvetjük. Miután már korábban
teszteltük, hogy a szórásokra fennáll a homogenitás, azaz a szórások egy közös
populáció szórásának becsléseiként foghatók fel, ezért az F próba
szignifikanciájából következik, hogy az átlagok nem egyetlen populáció várható
értékének becslései, azaz legalább egy átlag egy másik populációból származik,
azaz eltér a többitől.
Ha az ANOVA szignifikáns F értéket ad, akkor a további lépésekben a következő
technikákat használhatjuk::
-
Particionálás (Hatékonyabb, kevés összehasonlítás). Kontrasztokra dekomponálás
-
Előre meghatározott csoportokra tervezett többszörös összehasonlítások tesztjei
-
Minden lehetséges (páros) összehasonlításra vonatkozó többszörös
összehasonlítások tesztjei (páros összehasonlítások, vagy 3 és a fölötti
csoportból képezett kontraszt szignifikanciájának vizsgálata)
Különbséget kell tennünk az "a priori", és az "a posteriori", vagy
"post hoc" többszörös összehasonlítások között. Hatásfokuk, a próba ereje
mind különböző, és itt különösen hasznos a gondos kísérlettervezés.
ANOVA tábla
A végeredményt hagyományosan egy ANOVA
táblában foglalják össze.
Egyszeres osztályozás (egy szempontos variancia analízis, one-way ANOVA)
h darab kezelés, kezelésenként nem szükségképpen azonos esetszámmal
Lap teteje
I és II Modell
Ha elvetettük a H0-t, akkor a kérdés lehet, az átlagok, vagy a
szóródás eltérése miatt vetettük-e el.
Model I. 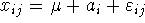 ahol az
ahol az 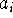 -k fix értékek, rögzített, fix és ismételhető hatások, a
kísérletező kontrollja alatt.
-k fix értékek, rögzített, fix és ismételhető hatások, a
kísérletező kontrollja alatt. 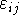 valószínűségi változó,
valószínűségi változó, 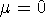 ,
rögzített érték.
,
rögzített érték.
Model II. 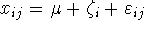 ahol
ahol 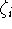 valószínűségi
változó,
valószínűségi
változó, 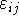 valószínűségi változó
valószínűségi változó 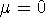 ,
rögzített érték.
,
rögzített érték.
A Modell II esetére példa: Genetikus és fenotipikus változékonyság,
családokon belül és között. Módszertani tanulmányok, minőségellenőrzés.
Lap teteje
H0 elvetése utáni analízis
Ekkor elővehetjük előzetes kérdéseinket, tovább elemezhetjük adatainkat,
vizsgálhatjuk előzetesen megfogalmazott statisztikai hipotéziseinket. Van arra
is módszer, hogy a kísérlet adatainak utólagos tanulmányozása során felmerült
kérdéseinket is statisztikai hipotézisvizsgálat tárgyává tegyük.
Előzetes kérdések (a priori) esete
-
Használhatjuk a Bonferroni, vagy a Holm féle eljárásokat a k előre elhatározott
összehasonlításra. Kis számú összehasonlításra jó hatásfokúak, nagyobb szám
esetében a többi alkalmazható eljáráshoz viszonyítva gyengébb hatásfokúak.
-
Ha h darab csoportunk van, és volt max. h-1 feltételezésünk (csak
egymástól függetlenek), akkor tervezett kontrasztokat vizsgálhatunk. Ez igen jó
hatásfokú analízis, jobb mint a többszörös összehasonlítások elvégzése. De nem
lehet az összes lehetséges páros összehasonlítást előre eltervezni, csak
egymástól függetlenek lehetnek, korlátozott számban. Pl. három csoport esetében
3 a lehetséges páros összehasonlítások száma, kettő tervezhető előre. Nagyobb
csoport számoknál az eltérés rohamosan nő! Több előre
tervezett (a priori) feltevésünk.
-
Használhatjuk a Dunn kontrasztokat (páros, vagy többes kontrasztokra) (A
STATISTICA program az eljárást nem tartalmazza, könnyen számolható, táblázattal
összevethető statisztikát eredményez)
-
Speciális eset: egy kontrollhoz több kezelés. Erre szolgál
a Dunnett-féle próba.
Az utóbbi esetben a Dunnett próbához az elemszámok aránya
optimalizálható. Ebben a kísérleti tervben nem az az optimális, ha minden
csoport egyforma elemszámú. A legjobb akkor a hatásfok, ha a kontroll csoportban
nagyobb az elemszám, mint az egyes kezelt csoportokban. Ennek az oka az, hogy a
kontroll csoport minden vizsgálandó összehasonlításban szerepel, érdemes róla
jobb hatásfokú becslést készíteni, mint az egyes "kezelt" csoportokra. Ha a
kezelt csoportok esetében az elemszám mind j, akkor a kontroll elemszáma
legyen j*négyzetgyök(m) .
Elemszámok a Dunnett-féle eljáráshoz
|
Csoport
|
Csoportok száma
|
Csoportokon belüli elemszám
|
|
Kontroll
|
1
|
j*négyzetgyök(m)
|
|
Kezelt
|
m
|
j
|
Lap teteje
Utólagos kérdések (a posteriori, post hoc) esete
Az adatok ismeretében, az adatok által sugallt kérdések megválaszolásához
használhatók, utólagos hipotézisek vizsgálhatók
-
Általános, sokcélú kontrasztok (kettőnél több csoportból is
képezhető): Scheffé, Tukey eljárásai
-
Páros összehasonlításokra (két tagú kontrasztok) Bonferroni t,
Sidak, Student-Neuman-Keuls, Tukey féle honest significant difference (HSD),
REGWF (Ryan, Einot, Gabriel, and Welsch F test, jobb mint a Scheffe, de ugyanúgy
nem tér el az ANOVA F hipotézisétől, azaz konzisztens).. Ezek mind alkalmas
eljárások.
-
Duncan féle teszt, és a LSD (least significant difference) módszer a
szignifikancia szint korrekciója nélkül
nem ajánlhatók, mert túl elnézőek, sokkal több hibához
vezethetnek, mint amit a névleges szignifikancia szint alapján
elképzelünk.
-
Bonferroni vagy Holm féle korrekcióval számított szigorúbb
szignifikancia szinttel végzünk páros összehasonlításokat (ekkor
felhasználhatjuk az LSD modul által adott számokat, mint a Holm eljárás során
vizsgálandó p értékeket), úgy, hogy ne haladjuk túl a kísérletenkénti 0.05, vagy
0.01 szignifikancia szintet. Ez az eljárás (különösen nagyobb csoportszámoknál)
eléggé konzervatív, növeli a másodfajú hibát, mert az "a posteriori"
alkalmazás esetén az összes lehetséges összehasonlítást kell a k értéknek
vennünk. Például a bevezetőben bemutatott 3 csoportos kísérletben a k=3
akkor is, ha utólagos döntéssel 2 összehasonlítást végzünk el (a lehetséges 3
független összehasonlításból).
Vegyes kérdések
Az ANOVA tervezhető mérete. Ne legyen 6-nál több faktor, 10-nél több szint.
Ne legyen túl sok függő változó.
A gyakorlatban az ANOVA elvégzése során 3 fázist kell végigcsinálni. A
statisztikai terv elkészítése, változók kijelölése, Kimenet megadása. Analízis,
részletek elemzése.
Lap teteje
Hasznos képletek
1. t próba
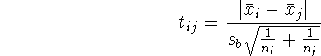
2. Dunn próba (többszörös összehasonlítás, tetszés szerinti kontrasztokra, a
priori eldöntött esetekre)

ahol 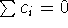 ,
sb
a közös szórásbecslés
,
sb
a közös szórásbecslés
Akkor használható, ha a tervezés szakaszában (az eredmények ismertté válása
előtt) eldöntik, melyek lesznek a kiszámítandó összehasonlítások. Nem elég
megmondani a darabszámot! A képletből kiszámított statisztikát Dunn cikkében
lévő táblázattal kell összevetni.
3. Dunnett próba (1 kontrollhoz hasonlítható az összes többi, de egymáshoz
nem)
k darab csoport, ahol az 1. számú a kontroll:

Egyenlőtlen elemszámoknál akkor optimális az elrendezés, ha
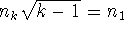 és
és 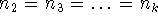
Más jelölésekkel ugyanezt mondja a fenti táblázat is. Az ANOVA közös
szórásbecslését használjuk (s)
4. Scheffé féle páros összehasonlítás (post hoc)
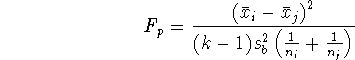
az i-edik és j-edik csoportok esetére. Az ANOVA közös
variancia
becslését használjuk
5. Scheffé féle kontraszt általános esete (három, vagy több csoport egy
kontrasztban történő
post hoc összehasonlítására)
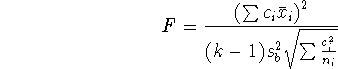
ahol 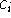 ortogonális kontrasztok koefficiensei, azaz
ortogonális kontrasztok koefficiensei, azaz 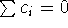
Az ANOVA közös variancia becslését használjuk. Egyenlőtlen csoportok
belüli elemszámok esetében is jól használható.
![]() ahol az
ahol az ![]() -k fix értékek, rögzített, fix és ismételhető hatások, a
kísérletező kontrollja alatt.
-k fix értékek, rögzített, fix és ismételhető hatások, a
kísérletező kontrollja alatt. ![]() valószínűségi változó,
valószínűségi változó, ![]() ,
rögzített érték.
,
rögzített érték.
![]() ahol
ahol ![]() valószínűségi
változó,
valószínűségi
változó, ![]() valószínűségi változó
valószínűségi változó ![]() ,
rögzített érték.
,
rögzített érték.
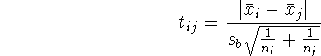

![]() ,
sb
a közös szórásbecslés
,
sb
a közös szórásbecslés

![]() és
és ![]()
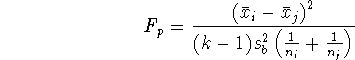
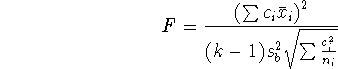
![]() ortogonális kontrasztok koefficiensei, azaz
ortogonális kontrasztok koefficiensei, azaz ![]()